彭罗斯阶梯是世界上非常著名的几何学悖论,彭罗斯阶梯指的是一个始终向上或向下但却无限循环的阶梯,彭罗斯阶梯其实有点像是盗墓剧《鬼吹灯》中悬魂梯,利用的其实就是一种几何学的原理,那么彭罗斯阶梯的原理到底是怎样的呢?

彭罗斯阶梯是一个有名的几何学悖论,指的是一个始终向上或向下但却无限循环的阶梯,可以被视为彭罗斯三角形的一个变体。这是一个由二维图形的形式表现出来的拥有4个90°拐角的四边形楼梯。由于它是个从不上升或下降的连续封闭循环图,所以一个人可以永远在上面走下去而不会升高。

彭罗斯阶梯最早是由瑞典艺术家Oscar Reutersvrd在1934年制作的,后由英国数学家罗杰·彭罗斯和父亲列昂尼德·彭罗斯设计并推广,并且在1958年2月《英国心理学月刊》中发表,据悉彭罗斯阶段的创作还是受到荷兰画家埃舍尔那些不可能出现于现实的诡异画面启发而创作的。
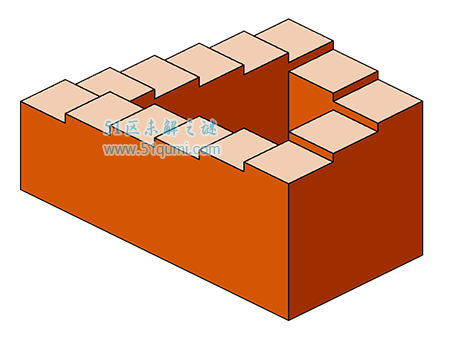
彭罗斯阶梯就是从基点再回到基点的一个过程,说白了就是一个上下过程。开始的时候你感觉是向上的行走,因为每阶楼梯的高度差一般都是大于底座坡度所引起的高度增长。当人到达中间的时候,你再上楼梯的时候,实际上就是每阶楼梯的高度差小于底座坡度所引起的高度增长。因此原本你觉得是在上楼,但是其实你的高度在逐渐的下降。
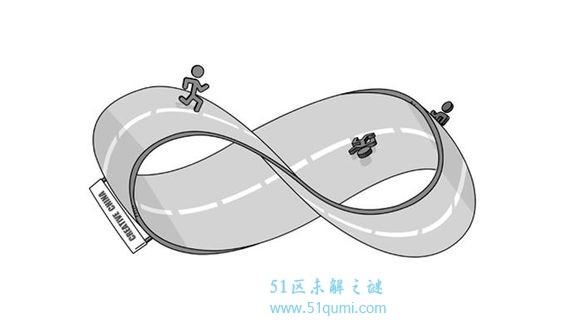
公元1858年,德国数学家莫比乌斯和约翰·李斯丁发现:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”。

克莱因瓶是一种无定向性的平面,比如二维平面就没有内外部之分,在拓扑学中克莱因瓶是一个不可定向的拓扑空间,1882年数学家菲利克斯·克莱因发现后命名,克莱因瓶的结构可表述为:一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。和我们平时用来喝水的杯子不一样,这个物体没有“边”,它的表面不会终结。它和球面不同 ,一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面,即它没有内外之分。
推荐阅读:
叫魂的过程是怎样?叫魂的原理是什么?
咬舌自尽真的可以吗?咬舌自尽的原理讲解
亚里士多德错觉原理是什么?你被它欺骗过吗?
滴血认亲的原理是什么?滴血认亲有科学依据吗?
标签:彭罗斯阶梯
相关推荐
